Funciones racionales:
- Funciones de proporcionalidad inversa:
Las funciones de proporcionalidad inversa son aquellas cuya expresión algebraica es :
y= k / x siendo k un número no nulo.
Propiedades de la función de
proporcionalidad inversa
§
Su dominio es R - {0}
§
En x=0 presentan una discontinuidad de salto infinito. Por tanto, eje Y, es
una asíntota vertical de la función.
§
El eje X es una asíntota horizontal.
§
Son crecientes si k <0 y decrecientes si k > 0.
§
No tienen puntos de corte con los ejes.
§
Sus ramas son simétricas respecto del origen de coordenadas, es una función
IMPAR.
§
Su representación gráfica es una hipérbola:
Ejemplo: Representa gráficamente la función y= 3/x
(Para ello, tenemos en cuenta todas las características
mencionadas antes, pero como en ellas no tenemos puntos destacables hay que hacer tabla de valores, como la gráfica está dividida en dos partes, hacemos dos tablas de valores; una para valores mayores que cero
y otra para valores menores que cero, la cual, por simetría respecto al origen,
tendrá las imágenes opuestas a las anteriores. Dibujamos la curva que pasa por
dichos puntos teniendo en cuenta las asíntotas).
- Funciones racionales del tipo:
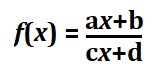
donde c y d no son cero simultáneamente.
Las gráficas de estas funciones también son hipérbolas, pero sus asíntotas ya no son los ejes de coordenadas (como en el caso de las de proporcionalidad inversa).
Propiedades de la función
§ Su dominio es R - {valor dónde se anula su denominador}
§ Tiene una asíntota vertical que pasa por el valor que le hemos quitado al dominio.
§ La asíntota horizontal es la recta y= a/c
§ Sí tienen puntos de corte con los ejes.
§ Sus ramas son simétricas respecto del punto dónde se cortan sus asíntotas
Para ver un ejemplo visualiza el siguiente vídeo que os he grabado, pincha en la imagen:
, donde m es la pendiente y P(x1, y1) son las coordenadas del punto.
