TRIÁNGULO DE TARTAGLIA

Ya hemos visto en clase de 4º cómo se construye el Triángulo de Tartaglia, también conocido como triángulo de Pascal,

 y la utilidad que tiene para calcular las potencias de un binomio, ya que todas las cifras escritas en cada fila del triángulo corresponden a los coeficientes del desarrollo de las potencias del binomio de Newton. 

Lo que a lo mejor no sabes es que este triángulo esconde dentro de sí varias curiosidades. Lo primero que te diré es que hace muchos años que se utiliza, no hay más que ver la siguiente imagen:

Triángulo de Shih-Chieh (1303)

En tercero de ESO vimos el número de oro, Φ , y su relación con la Sucesión de Fibonacci, que era aquella sucesión recurrente cuyos términos se obtenían sumando los dos anteriores, siendo los dos primeros términos igual a 1; es decir, 1, 1, 2, 3, 5, 8, 13, ..... Pues bien, los términos de esta sucesión aparecen en la suma de las diagonales del triángulo de Tartaglia:

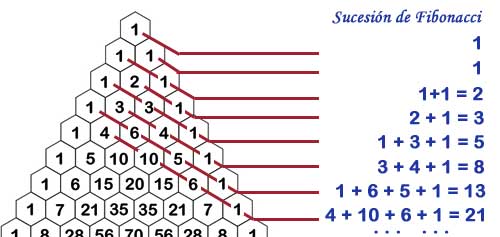
Pero...... si lo que sumamos son las filas, lo que obtenemos son ......

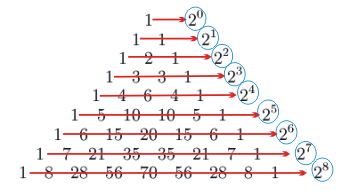
que puedes ver que son todas las potencias de base 2.

Pero, aún hay más, observa la siguiente imagen:

Te recuerdo lo que son los números triangulares: La sucesión 1, 3, 6, 10, …. Se llama sucesión de números triangulares, pues  pueden recomponerse para formar sucesivos triángulos equiláteros (como muestran los dibujos).

NOTA: Por convención, el primer número triangular es el 1, aunque con un punto no pueda formarse ningún triángulo.

Del mismo modo los números tetraédricos son la sucesión de números 1, 4, 10, 20, ... que pueden recomponerse para formar tetraedros:

Por último, os comento otra forma de construir el triángulo de Tartaglia y que  es mediante números combinatorios:

El número    se llama también número combinatorio. Se representa por  y se lee "m sobre n". Y es el número de subconjuntos de n elementos que pueden formarse con un conjunto de m elementos. 

Para calcular su valor se calcula mediante la siguiente expresión: 

siendo m! = m.(m-1).(m-2)....2.1 ( se lee m factorial)

Hay muchas más curiosidades dentro de este triángulo que te invito a descubrir en el libro El Diablo de los números , escrito en 1997 en alemán por Hans Magnus Enzensberger o viendo el siguiente vídeo:

FRACCIONES

Seguro que estás ya acostumbrado a utilizar expresiones como:

  "Dame un cuarto de Boquerones"   o   "Me he bebido un tercio de cerveza" o  "Compra medio queso",  pero ...... ¿sabes si antiguamente conocían las fracciones? ¿Qué civilizaciones las utilizaban? ¿Tenían símbolos especiales para ello?

Entre las tribus antiguas no parece haber existido prácticamente ninguna necesidad de usar fracciones; para las necesidades cuantitativas usuales el hombre puede elegir unidades lo suficientemente pequeñas como para evitar la necesidad de usar fracciones. Por lo tanto no hubo tampoco un progreso ordenado y lineal de las fracciones binarias a las quinarias y finalmente a las decimales, sino que los decimales fueron producto de la época moderna de la matemática y no del período antiguo.

En esta tabla puedes ver su evolución cronológica:




Vamos a ver algunas de las civilizaciones que las utilizaban y sus símbolos, empezaremos con los babilónicos.

Para ello puedes visualizar la siguiente presentación "Fracciones en el mundo babilónico"

Egipto

En el antiguo Egipto, el uso de las fracciones era algo muy común. En la tablilla de Ajmim y el papiro de Rhid, o papiro de Ahmes (este último que se encuentra en el museo de Londres desde el año 1865 y Data del año 1650 a.C) aparecen varios problemas y antecedentes que nos brindan una gran información sobre las matemáticas en el antiguo Egipto, aunque también se ha conseguido información sobre la matemática en Egipto a partir de tallados en piedras, inscripciones y calendarios. 

Los egipcios tenían una curiosa forma de representar las fracciones:

• Sólo utilizaban fracciones unitarias (con numerador 1), salvo casos excepcionales como la fracción 2/3 la cual tenía símbolo especial.
• El resto de fracciones las descomponían como suma de fracciones unitarias distintas:

            Por ejemplo 3/4 = 1/2 + 1/4

Para representar estas fracciones unitarias utilizaban un símbolo  parecido a un óvalo, que significaba parte, como muestra la figura:

                                            

Los chinos y las fracciones

Los chinos conocían muy bien las operaciones con fracciones ordinarias, hasta el punto de hallar el mínimo común denominador de varias fracciones. Como era su costumbre asignaban un rol femenino y otro masculino a los elementos que componen la fracción. Se referían al numerador como “el hijo” y al denominador como “ la madre”.  Más importante que estas curiosidades era, no obstante, la tendencia a la decimalización de las fracciones en China.  La adopción de un sistema decimal en pesos y medidas dio como resultado que se impusiera el hábito decimal en el manejo de las fracciones.

EL TAMGRAM

        El tangram es un rompecabezas de origen chino que probablemente apareció hace tan sólo 200 ó 300 años. Los chinos lo llamaron "tabla de sabiduría" y "tabla de sagacidad" haciendo referencia a las cualidades que el juego requiere. 

La misma palabra "tangram" es un invento occidental: Se supone que fue creada por un norteamericano aficionado a los rompecabezas, quien habría combinado tang, una palabra cantonesa que significa "chino", con el sufijo inglés gram (-grama) que significa "escrito" o "gráfico" (como en cardiograma).                                                                    

         Los primeros libros sobre el tangram aparecieron en Europa a principios del siglo XIX y presentaban tanto figuras como soluciones. Se trataba de unos cuantos cientos de imágenes en su mayor parte figurativas como animales, casas y flores... junto a una escasa representación de formas abstractas. A lo largo del siglo XIX aparecieron diversos libros de tangram chinos, que fueron copiados por las editoriales europeas, buena prueba de la popularidad que había adquirido el juego. A partir de 1818 se publicaron libros de tangram en EE. UU., Inglaterra, Francia, Alemania, Austria e Italia.

        En la introducción al libro publicado en Italia se hacía notar que el tangram se jugaba "en todas partes con verdadera pasión". En efecto, aunque una antigua enciclopedia china lo describía como "un juego de mujeres y niños", el tangram se había convertido en una diversión universal.

        En cuanto al número de figuras, la mayor parte de las publicaciones occidentales copiaron las figuras chinas originales, que ascendían a algunos cientos. Al principio el tangram fue publicado en forma de libro, en torno a 1870 se concedía más atención al juego mismo y sus siete componentes, de forma que el tangram era producido y vendido como un objeto: piezas de marfil, tarjetas con las siluetas y envoltorio en forma de caja.

        Hacia 1900 se habían añadido nuevas figuras y formas geométricas, llegando a un total de más de 900 y en 1973, los diseñadores holandeses Joost Elffers y Michael Schuyt produjeron una edición en rústica con 750 figuras nuevas, alcanzando así un total de más de 1.600. La edición de 1973 ha vendido hasta la fecha más de un millón de ejemplares en todo el mundo.

Puedes descargarte aquí tu plantilla para Tamgram, imprímela y recórtala.

Plantilla Tamgram

Estos son algunos ejemplos de figuras que puedes hacer con las piezas de un Tamgram, en ellas es fácil identificar la posición de las piezas. 

Cuando hayas practicado un poco te invito a que pruebes con las que están en negro, aquí tienes 120 posibles figuras, aunque existen muchas muchas más:

SUDOKU

¿Cómo?
¿Que aún no has resuelto nunca un Sudoku?
¿Qué nadie te ha explicado cómo se hacen?

Pues te invito a hacerlo ahora mismo.

Primero te daré las instrucciones:

Regla 1: hay que completar las casillas vacías con un solo número del 1 al 9.

Regla 2: en una misma fila no puede haber números repetidos.

Regla 3: en una misma columna no puede haber números repetidos.

Regla 4: en una misma región no puede haber números repetidos.

Regla 5: la solución de un sudoku es única.

Te invito a ponerte a prueba. Empieza por el más fácil y ...... ¡ a ver si eres capaz de llegar a resolver el más difícil de todos!